This article is evolving. A whole lot of subnets are planned to be launched this year. This begs the question: what can be done, if anything, to leverage their existence to further boost their individual security, effectively cross-pollinating state and validators? I’ll try to go through a few options below. Note that this isn’t meant to be an exhaustive review. Background and Definitions

First, some background material. For those unfamiliar, subnets are the latest generation of blockchains. In the most generic term, subnets are generic chains with two key properties:

• The validators of the subnet are publicly known and are also validators of the Avalanche primary subnet
• The validators of the subnet can efficiently communicate and execute instructions with the validators of any other subnet

This is a powerful construction, because it both a) enables development independence, while b) enabling efficient and trivial interoperability. The subnet can be customized through pre-compiles, including delegator fees, token supplies, and more.

After instantiation, a subnet communicates efficiently with the rest of the network through the AWM protocol, which leverages the use of BLS signatures, as shown below:

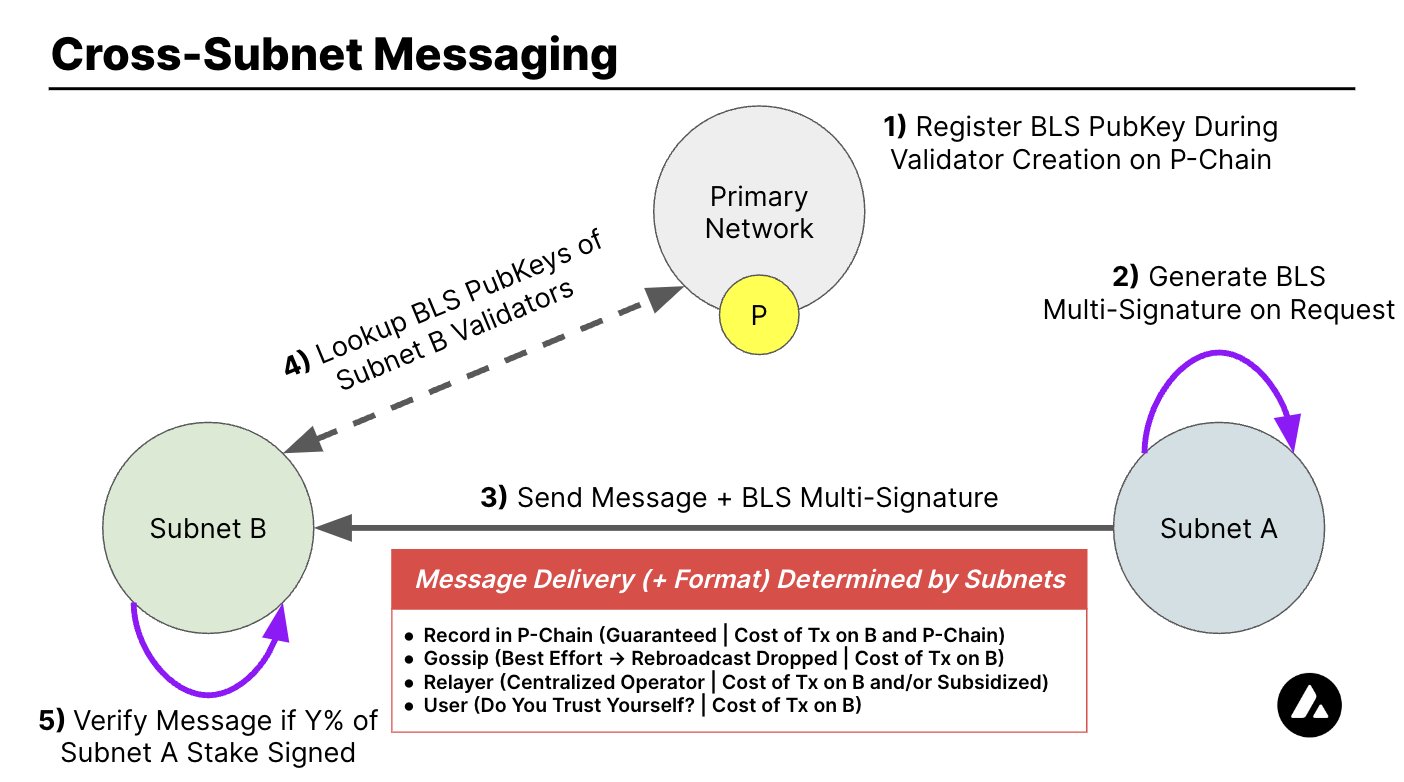
In order for the AWM protocol to work, you require a special metadata chain to securely share information about who’s staking at any given time. As it turns out, this is exactly what the P-chain primary subnet does.

Note the key feature here: communication does not need to happen through the primary subnet. It is done efficiently subnet to subnet.

Formal Definitions

A “blockchain (chain)” is a replicated database, or – more formally – a replicated state machine, that is maintained across a set of validators \(\{v_1, v_2, … v_n\}\). The chain has some state, and it takes inputs in the form of transactions. Note that the chain can become corrupted (i.e. the validators no longer are able to recreate the canonically correct representation of the latest set of inputs to the state machine), and if so, the only recourse is social consensus. This is a failure at the protocol level.

A “subnet” is a special blockchain wherein the set of validators is not just known to the set \(\{v_1, v_2, … v_n\}\), but it is also known publicly by the world, encoded in a special global metadata chain.

I will use the expanded form \(v(k)_i\) to represent the “i”-th validator of chain “k”.

Cross subnet state checkpointing

The most direct (and arguably cleanest) solution would be to encode compact state hashes from one subnet to another. Since the AWM protocol doesn’t need to write data on the primary subnet, we could directly encode. Of course, the downside to this is that it would assume that the secondary subnet is never corrupted. The protocol is very simple: the validators of the first subnet generate a new root hash, which is signed by \(\{v(a)_1, v(a)_2 …, v(a)_n\}\), and then written as a contract transaction to the second subnet, which produces simple verification proofs on the P-chain. If the secondary subnet is not trusted to not misbehave ever, the transaction could instead be encoded into the primary subnet, albeit it would be more expensive.

The obvious pros of this protocol are that it is efficient and cheap. The cons are that the checkpointing includes only a hash, and therefore the network is susceptible to data loss should both subnets become corrupted. Should concerns over data loss arise, one can upgrade the protocol to include data replication, i.e. include the entire state. Naturally, the issue is the sheer expense.

Cross subnet validation

Even if you were to checkpoint the entire state of subnet “a” to subnet “b”, you might be still concerned with the subnet becoming corrupted in the first place. The natural solution here is to boost the validation using existing validators of another subnet. Therefore, not only will the secondary subnet be able to serve as a checkpointing mechanism, it will also serve as a validation mechanism. The trivial way of doing this is to enable the second subnet to act as a light client on the first subnet. At that point, finality is the totality of \(\{v(a)_1, v(a)_2 …, v(a)_n\}\) and \(\{v(b)_1, v(b)_2 …, v(b)_m\}\).